算法之复杂度分析

一、什么是复杂度分析

数据结构与算法解决的是如何让计算机更快时间、更省空间的解决问题，因此需从执行时间和占用空间两个维度来评估数据结构和算法的性能。

算法用时间复杂度和空间复杂度两个概念来描述性能问题，二者统称为复杂度。复杂度描述的是算法执行时间（或占用空间）与数据规模的增长关系。而复杂度分析用来计算代码的执行效率，和性能测试相比，复杂度分析有不依赖执行环境、成本低、效率高、易操作、指导性强的特点。

二、复杂度的表示方式

用大 O 表示法来表示复杂度，例如：

T(n) = O(f(n))
S(n) = O(f(n))

• T：算法需要执行的总时间；
• S：算法需要的总空间；
• f(n)：代码执行的总次数。

举个例子：

function go(n) {
  var item = 0;                   // 这里执行了 1 次
  for (var i = 0; i < n; i++) {   // 这里执行了 n 次
    for (var j = 0; j < n; j++) { // 这里执行了 n*n 次
      item = item + i + j;        // 这里执行了 n*n 次
    }
  }
  return item;                    // 这里执行了 1 次
}

上面这段代码的总执行时间为 1+n+n×n+n×n+1 = 2+n+2n²

也就是说 T(n) = O(f(2+n+2n²))

这就是大 O 时间复杂度表示法，它不代表代码真正的执行时间，而是表示代码随数据规模增长的变化趋势，简称时间复杂度。

另外，当 n 很大时，可以忽略常数项，只保留一个最大量级即可。所以上面的代码执行时间可以简单标记为 T(n) = O(n²)

三、时间复杂度的分析方式

算法的时间复杂度表示算法的执行时间根据数据规模增长的一个趋势，并非代码的执行时间。

1、只需关注循环最多的代码块

在分析的时候，只需要关心哪个代码块循环次数最多，举个例子：

function total(n) {             // 第 1 行
  var sum = 0;                  // 第 2 行
  for (var i = 0; i < n; i++) { // 第 3 行
    sum += i;                   // 第 4 行
  }                             // 第 5 行
}                               // 第 6 行

上面代码中，循环最多的代码块是 3、4 行，循环都是 n 次，所以时间复杂度就是 O(n)

2、最大值原则

最大值原则，指的是总复杂度等于量级最大的代码块复杂度，举个例子：

function total(n) {
  // 第一个 for 循环
  var sum1 = 0;
  for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++) {
      sum1 = sum1 + i + j;
    }
  }
  // 第二个 for 循环
  var sum2 = 0;
  for (var i = 0; i < 1000; i++) {
    sum2 = sum2 + i;
  }
  // 第三个 for 循环
  var sum3 = 0;
  for (var i = 0; i < n; i++) {
    sum3 = sum3 + i;
  }
}

上面的代码，可以先分别分析每段 for 循环的时间复杂度，再取其中最大的量级来作为整段代码的时间复杂度。

• 第一个 for 循环的时间复杂度：O(n²)
• 第二个 for 循环的时间复杂度：循环执行了 1000 次，是个常数量级，尽管对代码的执行时间会有影响，但是当 n 无限大时可以忽略。
• 第三个 for 循环的时间复杂度：O(n)

综上，上面代码的时间复杂度为 O(n²)

3、乘法原则

乘法原则，指的是嵌套代码复杂度等于嵌套内外代码复杂度乘积，举个例子：

function f(i) {
  var sum = 0;
  for (var j = 0; j < i; j++) {
    sum += j;
  }
  return sum;
}

function total(n) {
  var res = 0;
  for (var i = 0; i < n; i++) {
    res = res + f(i); // 调用 f 函数
  }
}

上面代码中，total 方法时间复杂度 O(n)，f 方法的时间复杂度 O(n)，所以整段代码的时间复杂度为 O(n²)

四、常见的时间复杂度分析

只看最高量级的复杂度，下面按效率从高到低依次划分：

操作数量实例	大 O 表示法	术语
2	O(1)	常数阶
2㏒n	O(㏒n)	对数阶
2n + 1	O(n)	线性阶
2n² + n + 1	O(n²)	平方阶
2n³ + n + 1	O(n³)	立方阶
2ⁿ + 1	O(2ⁿ)	指数阶
n! + 1	O(n!)	阶乘阶

上面可以分为多项式量级和非多项式量级。其中，非多项式量级为 O(2ⁿ) 和 O(n!)

对应的增长率如下图：

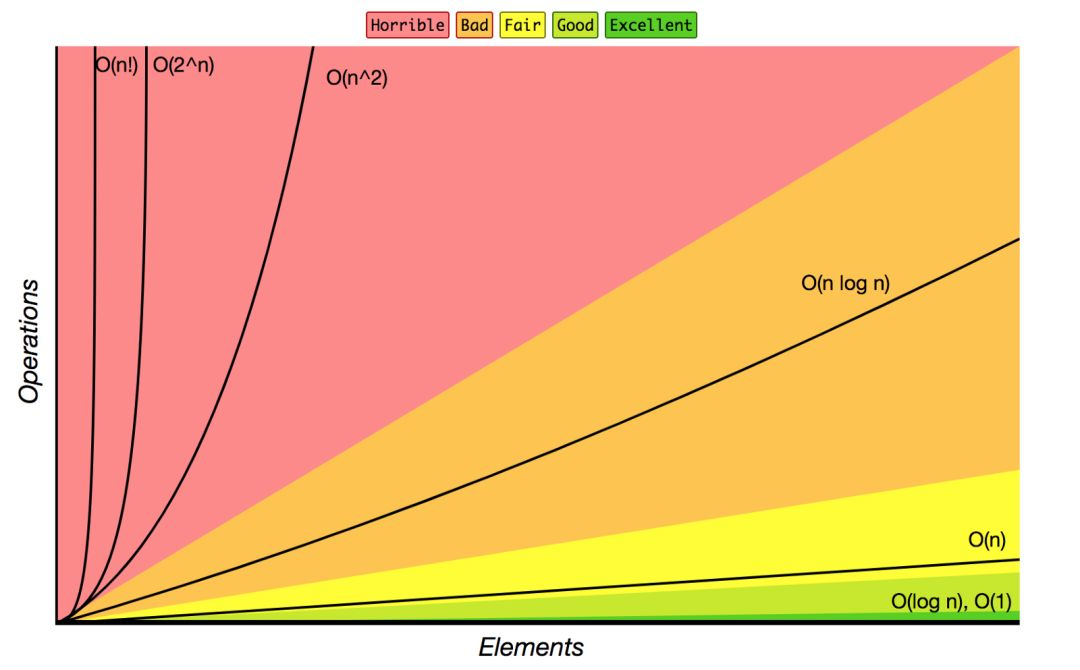
可以看到，当数据规模 n 增长时，非多项式量级的执行时间就会急剧增加，所以非多项式量级的代码算法是非常低效的。

1、常数阶复杂度 O(1)

O(1) 只是常量级时间复杂度表示法，并不是代码只有一行，举个例子：

function total() {
  var sum = 0;
  for (var i = 0; i < 100; i++) {
    sum += i;
  }
}

虽然有这么多行，且 for 循环执行了 100 次，但代码的执行时间不随 n 的增大而增长，所以这样的代码复杂度就为 O(1)

2、对数阶 O(㏒n) 和 O(n㏒n)

举个对数阶时间复杂度的例子:

function total1(n) {
  var sum = 0;
  var i = 1;
  while (i <= n) {
    sum += i;
    i = i * 2;
  }
}

function total2(n) {
  var sum = 0;
  for (var i = 1; i <= n; i = i * 2) {
    sum += i;
  }
}

上面函数 total1 和 total2 有一个相同点：变量 i 从 1 开始取值，每循环一次乘以 2，当大于 n 时，循环结束。实际上，i 的取值就是一个等比数列，如果设 x 为循环次数，则 i 的值为：

2º 2¹ 2² ... 2ᵏ... 2ˣ = n;

由 2ˣ = n 可以得出循环次数 x = ㏒₂n，所以这两个函数的时间复杂度为 O(㏒₂n)

时间复杂度的分析可以忽略常数，也可以忽略对数中的底数，所以上面的对数阶复杂度可以表示为 O(㏒n)，而 O(n㏒n) 则表示时间复杂度为 O(㏒n) 的代码执行了 n 次。

3、其他复杂度 O(m+n) 和 O(m*n)

举个例子：

function total(m, n) {
  var sum1 = 0;
  for (var i = 0; i < n; i++) {
    sum1 += i;
  }
  var sum2 = 0;
  for (var i = 0; i < m; i++) {
    sum2 += i;
  }
  return sum1 + sum2;
}

因为无法评估 m 和 n 谁的量级比较大，所以不能忽略掉任何一个，这个函数的复杂度是有两个数据的量级来决定的，所以此函数的时间复杂度为 O(m+n)，O(m*n) 的时间复杂度同理。

五、空间复杂度分析

空间复杂度表示算法的存储空间和数据规模之间的关系，推算方式与时间复杂度类似。

举个例子：

/** O(1) **/
let i = 0;
i += 1;

/** O(n) **/
const arr = [];
for (let i = 0; i < n; i++) {
  arr.push(i);
}

/** O(n²) **/
const matrix = [];
for (let i = 0; i < n; i++) {
  matrix.push(i);
  for (let j = 0; j < n; j++) {
    matrix[i].push(j);
  }
}

如上面代码，常见的空间复杂度有 O(1)、O(n)、O(n²)，其余情况则比较少见。

六、复杂度优化

下面的代码很容易知道时间复杂度为 O(n)

function total(n) {
  var sum = 0;
  for (var i = 1; i <= n; i++) {
    sum += i;
  }
  return sum;
}

由于上面是一个等差数列求和，等差数列求和公式如下：

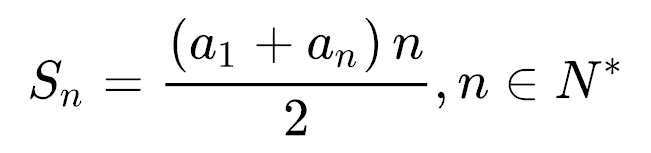
所以如果想把复杂度降到常数阶 O(1)，可以这么操作：

function total(n) {
  var sum = (n * (n + 1)) / 2;
  return sum;
}

七、总结

复杂度也叫渐进复杂度，包括时间复杂度和空间复杂度，一个表示执行的快慢，一个表示内存的消耗，用来分析算法执行效率与数据规模之间的增长关系，可以粗略的表示，越高阶复杂度的算法，执行效率越低。