Skip to main content

树的定义及实现

1. 树的定义​

树形数据结构是一类重要的非线性数据结构，可以表示数据之间一对多的关系。

1.1 树的作用​

树结构对比于数组/链表/哈希表有以下优势：

与数组对比：

  • 优点：数组可以通过下标直接访问元素，访问效率更高。
  • 缺点：数组在查找特定数据时，需要先将数据进行排序，生成有序数组，这样才能提高查找效率。此外，在插入或删除元素时，可能需要移动大量其他元素，导致效率较低。

与链表对比：

  • 优点：链表插入和删除数据时效率很高，因为只需调整指针，不需要移动其他元素。
  • 缺点：链表查找特定数据时效率较低，需要从头开始逐个查找，直到找到目标。此外，在链表的中间位置插入或删除数据时，虽然效率高，但整体操作仍然相对复杂。

与哈希表对比：

  • 优点：哈希表在插入、查询和删除操作时效率极高，能快速找到需要的数据。
  • 缺点：哈希表空间利用率较低，因为底层数组中的很多单元可能没有被使用。同时，哈希表中的元素是无序的，无法按照固定顺序遍历。此外，无法快速找出哈希表中的最大值或最小值等特殊值。

树结构综合了上述三种结构的优点，同时也弥补了它们存在的缺点（虽然效率不一定都比它们高），比如树结构中数据都是有序的，查找效率高；空间利用率高；并且可以快速获取最大值和最小值等。

1.2 树的基本术语​

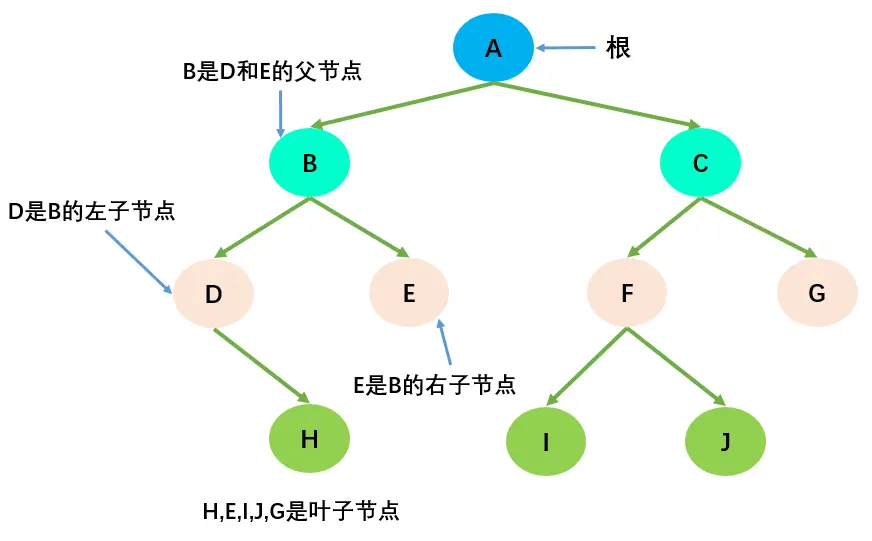
  • 节点的度（Degree）：节点的子树个数，比如节点 B 的度为 2；
  • 树的度：树的所有节点中最大的度数，如上图树的度为 2；
  • 叶节点（Leaf）：度为 0 的节点（也称为叶子节点），如上图的 H、I 等；
  • 父节点（Parent）：度不为 0 的节点称为父节点，如上图节点 B 是节点 D 和 E 的父节点；
  • 子节点（Child）：若 B 是 D 的父节点，那么 D 就是 B 的子节点；
  • 兄弟节点（Sibling）：具有同一父节点的各节点彼此是兄弟节点，比如上图的 B 和 C，D 和 E 互为兄弟节点；
  • 路径和路径长度：路径指的是一个节点到另一节点的通道，路径所包含边的个数称为路径长度，比如 A→H 的路径长度为 3；
  • 节点的层次（Level）：规定根节点在 1 层，其他任一节点的层数是其父节点的层数加 1。如 B 和 C 节点的层次为 2；
  • 树的深度（Depth）：树中所有节点中的最大层次是这棵树的深度，如上图树的深度为 4；

2. 二叉树​

如果树中的每一个节点最多只能由两个子节点，这样的树就称为二叉树；

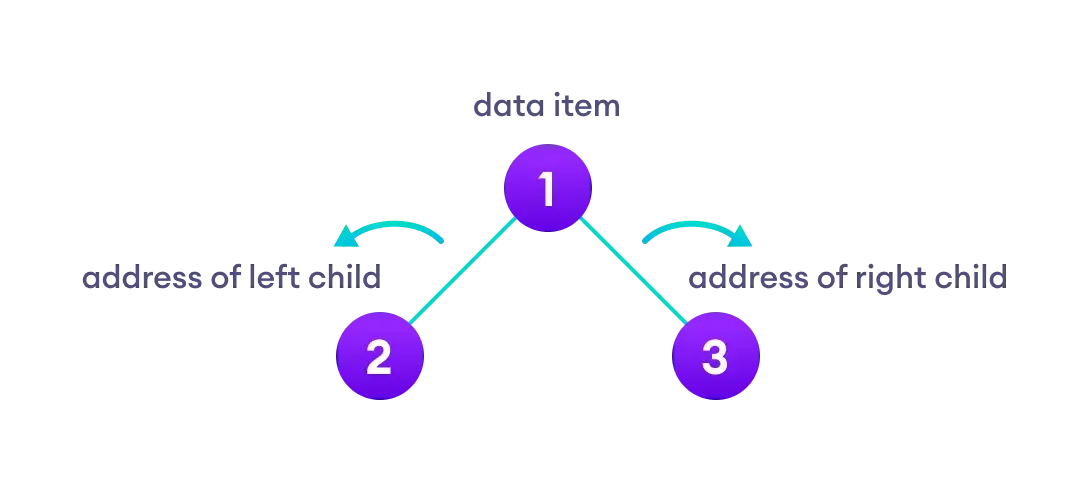
2.1 二叉树的分类​

2.1.1 完美二叉树​

完美二叉树（Perfect Binary Tree）中每个内部节点恰好有两个子节点，而所有叶节点都处于同一级别：

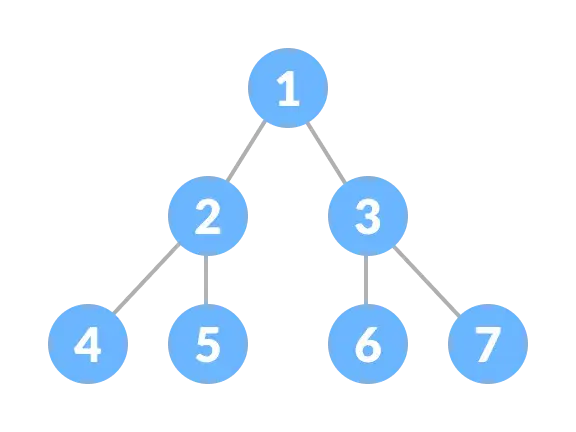
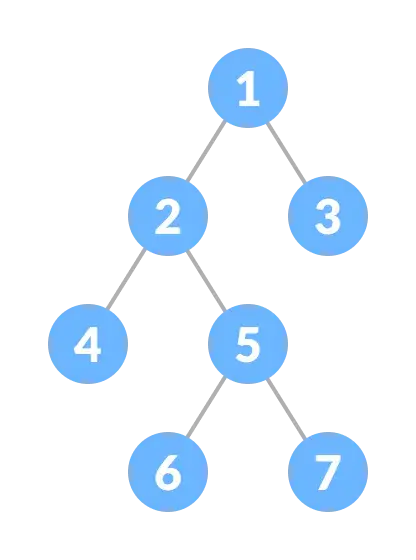
2.1.2 满二叉树​

满二叉树（Full Binary Tree）是二叉树的一种特殊类型，其中每个父节点/内部节点都有两个或没有子节点：

2.1.3 完全二叉树​

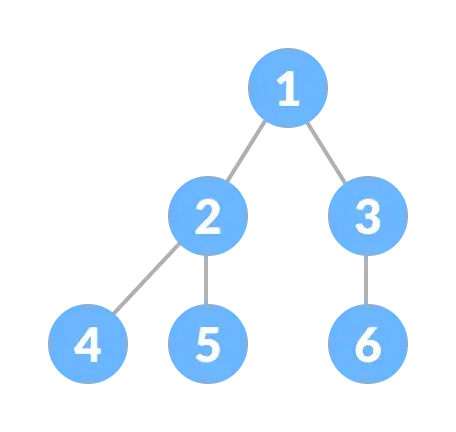
完全二叉树类似满二叉树，但有区别：

  1. 每一层必须完全填满：除了最后一层，所有层的节点都必须达到最大数量；
  2. 叶子节点向左倾斜：所有的叶子节点都必须集中在左侧，即使最后一层没有完全填满，也要从左到右依次排列；
  3. 最后一层的叶子节点可能不齐全：完全二叉树的最后一层可以缺少一些节点，但这并不影响它的定义，因此完全二叉树不一定是满二叉树。

2.2 二叉树的遍历​

2.2.1 前序遍历​

  1. 访问根节点
  2. 访问左侧子树中的所有节点
  3. 访问右侧子树中的所有节点
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *   this.val = (val===undefined ? 0 : val)
 *   this.left = (left===undefined ? null : left)
 *   this.right = (right===undefined ? null : right)
 * }
 */

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
const preorderTraversal = (root) => {
  let result = []
  const preorder = (node) => {
    if (!node) return
    // 先根节点
    result.push(node.val)
    // 然后遍历左子树
    preorder(node.left)
    // 再遍历右子树
    preorder(node.right)
  }
  preorder(root)
  return result
};

2.2.2 中序遍历​

  1. 首先，访问左侧子树中的所有节点
  2. 然后是根节点
  3. 访问右侧子树中的所有节点
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *   this.val = (val===undefined ? 0 : val)
 *   this.left = (left===undefined ? null : left)
 *   this.right = (right===undefined ? null : right)
 * }
 */

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
const inorderTraversal = function (root) {
  const result = []
  const inorder = node => {
    if (!node) return
    inorder(node.left)
    result.push(node.val)
    inorder(node.right)
  }
  inorder(root)
  return result
};

2.2.3 后序遍历​

  1. 访问左侧子树中的所有节点
  2. 访问右侧子树中的所有节点
  3. 访问根节点
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *   this.val = (val===undefined ? 0 : val)
 *   this.left = (left===undefined ? null : left)
 *   this.right = (right===undefined ? null : right)
 * }
 */

/**
 * @param {TreeNode} root
 * @return {number[]}
 */
const postorderTraversal = function (root) {
  const result = []
  const postorder = node => {
    if (!node) return
    postorder(node.left)
    postorder(node.right)
    result.push(node.val)
  }
  postorder(root)
  return result
};

2.2.4 层序遍历（广度优先遍历）​

层序遍历 BFS，顾名思义就是按树的深度，从根节点开始，一层一层向底部遍历：

代码实现如下：

const bfs = root => {
  const queue = []
  if (root) queue.push(root)
  while (queue.length) {
    const curNode = queue.shift()
    console.log(curNode.val)
    curNode.children.forEach(child => {
      queue.push(child)
    })
  }
}
bfs(tree)