Skip to main content

JS 数字精度丢失及处理

一、精度丢失的场景​

0.1 + 0.2 === 0.3 // false

0.1 + 0.1 // 0.2
0.1 + 0.2 // 0.30000000000000004
0.1 + 0.3 // 0.4

上面出现 false 是因为 0.1 + 0.2 的结果是 0.30000000000000004，为什么会这样呢？

二、原因分析​

1、二进制与十进制的转换​

1-1、十进制转二进制​

除 2 取余，逆序排列

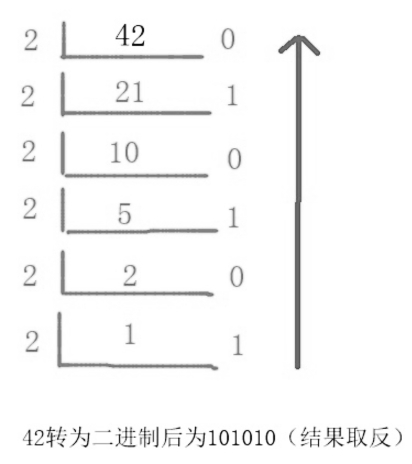
举个例子，42 转二进制：

1-2、二进制转十进制​

从右到左用二进制的每个数去乘以 2 的对应次方（从 0 开始）

举个例子，00101010 转十进制：

2、计算机的二进制存储​

计算机存储双精度浮点数时，需要先把十进制数转为二进制的科学记数法形式，然后计算机以自己的规则 {符号位 + (指数位 + 指数偏移量的二进制) + 小数部分} 存储二进制的科学记数法。

由于存储的位数有限（64位），且一些十进制浮点数在转为二进制数时会出现无限循环，造成二进制的舍入操作，当再转为十进制时就造成了计算误差。举个例子：

  • 27.5 转换为二进制 11011.1
  • 11011.1 转换为科学记数法：
  • 符号位为 1(正数)，指数位为 4+，1023+4，即 1027，因为它是十进制的需要转换为二进制，即 10000000011，小数部分为 10111，补够 52 位即： 1011 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

所以 27.5 存储为计算机的二进制标准形式（符号位+指数位+小数部分 (阶数)）为：

0+10000000011+011 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

回到上面 0.1 + 0.2：

// 0.1 和 0.2 都转化成二进制后再进行运算
0.00011001100110011001100110011001100110011001100110011010 +
0.0011001100110011001100110011001100110011001100110011010 =
0.0100110011001100110011001100110011001100110011001100111

// 转成十进制正好是 0.30000000000000004

三、解决方式​

1、toPrecision​

使用 toPrecision 控制精度，以 12 为精确位数，可以解决大部分 0001 和 0009 的问题，例如：

parseFloat(1.4000000000000001.toPrecision(12)) === 1.4  // true

对于加减乘除，则不能直接用 toPrecision 来控制了，可以把小数转为整数后再运算，以加法为例：

/**
 * 精确加法
 */
function add(num1, num2) {
  const num1Digits = (num1.toString().split('.')[1] || '').length;
  const num2Digits = (num2.toString().split('.')[1] || '').length;
  const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));
  return (num1 * baseNum + num2 * baseNum) / baseNum;
}

2、mathjs​

可直接使用 mathjs 解决精度问题：

const ans = math.add(0.1, 0.2)     //  0.30000000000000004
math.format(ans, {precision: 14})  // '0.3'

3、number-precision​

number-precision 也可用于解决精度问题：

import NP from 'number-precision'

NP.strip(0.09999999999999998); // = 0.1
NP.plus(0.1, 0.2);             // = 0.3, not 0.30000000000000004
NP.plus(2.3, 2.4);             // = 4.7, not 4.699999999999999
NP.minus(1.0, 0.9);            // = 0.1, not 0.09999999999999998
NP.times(3, 0.3);              // = 0.9, not 0.8999999999999999
NP.times(0.362, 100);          // = 36.2, not 36.199999999999996
NP.divide(1.21, 1.1);          // = 1.1, not 1.0999999999999999
NP.round(0.105, 2);            // = 0.11, not 0.1