V8 引擎数组排序算法

Chrome 的 V8 引擎数组排序采用的算法取决于数组长度，当数组长度小于等于 10 采用插入排序，大于 10 采用快速排序。

一、插入排序

1、插入排序的原理

插入排序将第一个元素视为有序序列，遍历数组，将之后的元素依次插入这个构建的有序序列中。

当数组长度较小时，使用插入排序效率更高。

2、插入排序的时间复杂度

• 最好情况：数组升序排列，时间复杂度为：O(n)
• 最坏情况：数组降序排列，时间复杂度为：O(n²)

3、插入排序的稳定性

算法稳定性

稳定算法指的是排序前后两个相等的数相对位置不变。

不稳定算法有：

• 堆排序
• 希尔排序
• 快速排序
• 选择排序

插入排序的过程：

1. 已经有序的小序列的基础上，一次插入一个元素；
2. 要插入的元素和已经有序的最大者开始比，如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置；
3. 如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面；
4. 相等元素的前后顺序没有改变；

因此，插入排序是稳定算法。

4、插入排序的实现

function insertionSort(arr) {
  for (var i = 1; i < arr.length; i++) {
    var element = arr[i];
    for (var j = i - 1; j >= 0; j--) {
      var tmp = arr[j];
      var order = tmp - element;
      if (order > 0) {
        arr[j + 1] = tmp;
      } else {
        break;
      }
    }
    arr[j + 1] = element;
  }
  return arr;
}

const arr = [6, 5, 4, 3, 2, 1]; // [1, 2, 3, 4, 5, 6]
console.log(insertionSort(arr));

二、快速排序

1、快速排序的原理

1. 选择一个元素作为基准；
2. 小于基准的元素移到基准左边；大于基准的元素移到基准右边；
3. 对基准左边和右边的两个子集，不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

举个例子，对数组 [85, 24, 63, 45, 17, 31, 96, 50] 快速排序：

• 第一步，选择中间的元素 45 作为基准（基准值可以任意选择，但选择中间的值比较容易理解）

• 第二步，按照顺序，将每个元素与基准进行比较，形成两个子集，一个小于 45，另一个大于等于 45：

• 第三步，对两个子集不断重复第一步和第二步，直到所有子集只剩下一个元素为止：

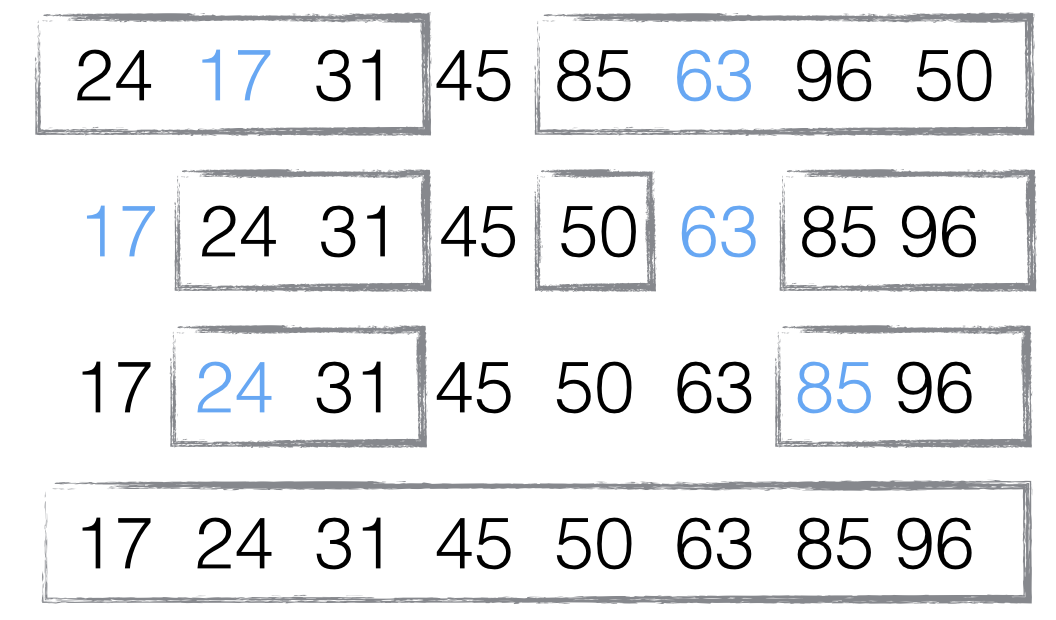
2、快速排序的时间复杂度

快速排序的关键点就在于基准的选择，选取不同的基准时，会有不同性能表现。

一般情况下快速排序的时间复杂度是 O(𝑛㏒𝑛)，最坏情况是 O(𝑛²)

• 最好的情况：每一次都平分整个数组，划分产生的两个子问题分别包含 𝑛/2 和 𝑛/2 − 1 个元素，算法需要执行的总时间 𝑇(𝑛) = 2𝑇(𝑛/2) + O(𝑛)，解为 𝑇(𝑛) = O(𝑛㏒𝑛)
• 最坏的情况：每次选择基准元素时总是选择第一个元素或最后一个元素，当划分产生的两个子问题分别包含 n-1 和 0 个元素，划分操作的时间复杂度为 O(𝑛)，𝑇(0) = O(1)，这时算法需要执行的总时间 𝑇(𝑛) = 𝑇(𝑛−1) + 𝑇(0) + O(𝑛) = 𝑇(𝑛−1) + O(𝑛)，解为 𝑇(𝑛) = O(𝑛²)

V8 引擎为了提高性能，对基准的选择做了很多优化。

V8 选择基准的原理

• 当数组长度大于 10 但小于 1000 时，取中间位置的元素：

// 基准的下标
// >> 1 相当于除以 2 (忽略余数)
third_index = from + ((to - from) >> 1);

• 当数组长度大于 1000 时，每隔 200 ~ 215 个元素取一个值，然后将这些值进行排序，取中间值的下标：

function GetThirdIndex(a, from, to) {
  var t_array = new Array();

  // & 表示是按位与运算符
  // 对整数操作数逐位执行布尔与操作
  // 只有两个操作数中相对应的位都是 1，结果中的这一位才是 1
  // 以 15 & 127 为例：
  // 15 二进制为 （0000 1111）
  // 127 二进制为（1111 1111）
  // 按位与结果为 （0000 1111）＝ 15
  // 所以 15 & 127 的结果为 15
  // 注意 15 的二进制为 1111
  // 这就意味着任何和 15 按位与的结果都会 ≤ 15，这才实现了每隔 200 ~ 215 个元素取一个值
  var increment = 200 + ((to - from) & 15);

  var j = 0;
  from += 1;
  to -= 1;

  for (var i = from; i < to; i += increment) {
    t_array[j] = [i, a[i]];
    j++;
  }
  // 对随机挑选的这些值进行排序
  t_array.sort(function (a, b) {
    return comparefn(a[1], b[1]);
  });
  // 取中间值的下标
  var third_index = t_array[t_array.length >> 1][0];
  return third_index;
}

3、快速排序的稳定性

快速排序的过程：

1. 以数组 [1, 2, 3, 3, 4, 5] 为例；
2. 假如选定了第 3 个元素 (3) 为基准，< 3 的在基准前面，≥ 3 的在后面，排序的结果没有问题；
3. 如果选择了第 4 个元素 (第二个 3 )，< 3 的在基准前面，≥ 3 的在后面，第一个 3 就会被移到第二个 3 后面。

因此，快速排序是不稳定算法。

4、快速排序的实现

const quickSort = (arr) => {
  const len = arr.length;
  if (len < 2) {
    return arr;
  } else {
    // 选标尺元素
    const flag = arr[0];
    const left = [];
    const right = [];
    // 把剩余的元素进行遍历，比标尺元素小的放左边，大的放右边
    for (let i = 1, temp; i < len; i++) {
      temp = arr[i];
      if (temp < flag) {
        left.push(temp);
      } else {
        right.push(temp);
      }
    }
    // 进行递归操作
    return quickSort(left).concat(flag, quickSort(right));
  }
};

三、插入排序与快速排序比较

点击查看所有排序性能图示